1. Home
  2. Electrical and Electronics Calculators
  3. Ohm's Law Calculator

Ohm's Law Calculator

Enter any two known circuit parameters in the below Ohm's law calculator and calculate the remaining two values according to Ohm's Law.

Volt
Watts

 
 

 

 

Ohms law is the most fundamental law that governs the relationship between Voltage (V), Current (I), and Resistance(R). It was define by the German scientist Georg Simon Ohm, and hence is named after him. The law states that “for any circuit the electric current (I) is directly proportional to the voltage (V) and is inversely proportional to the resistance(R)”.

This is the most fundamental law from which all other concepts were derived; perhaps this will be the first law that is introduced to anyone who is interested in electronics. The concept behind this law is very simple it simply means that the Voltage across any two points in a circuit will always equal to the product of the Resistance between the two points and the current flowing through the circuit. This can be mathematically given by

V = IR

Where, V=Voltage I=Current and R=Resistance

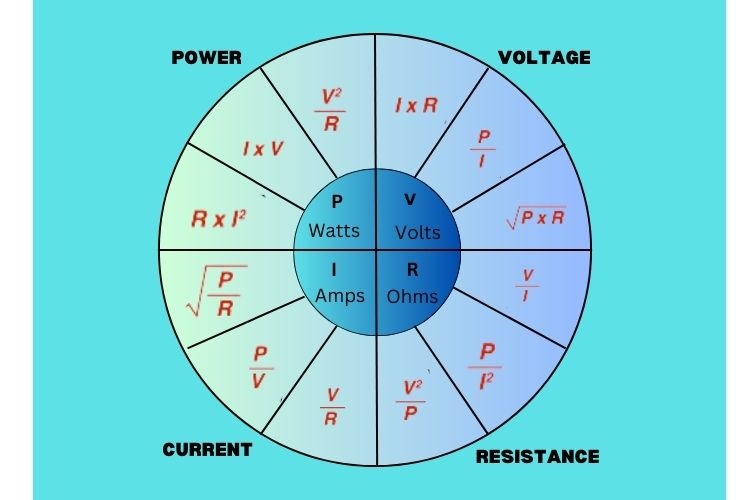
ohms law calculator formulae

This formula can also be re-written into following forms

V=IR

I=V/R

R = V/I
 
Using these three formulae you can calculate the value of Voltage, Current or Resistance. Once you know either of these two parameters you can also calculate the power using the below formulae

P=VI

P=I2R

P= V2/R
 

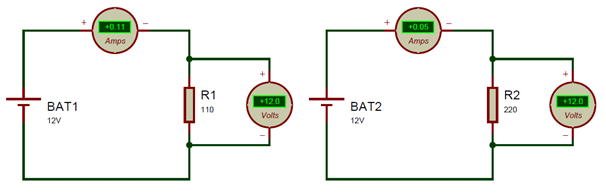
Ohms law calculation in circuits

Let us test our ohms law principle on the above two circuits. The voltage source for both the circuit is 12V. But we have two different resistance values for circuits, the one on the left uses 110Ω and the one on the right uses 220Ω.

Let us calculate the current that should flow through the circuit for both circuits. We know the formulae I = V/R.

For the left side Circuit I = V/R which is I = 12/110 and that gives us 0.109A which is ~0.11A, if check it using the ammeter (refer ammeter in above pic) we will get the dame value.

For the right side Circuit I = 12/220 and that gives us 0.54A which is ~0.5A, if check it using the ammeter (refer ammeter in above pic) we will get the dame value.

Similarly you can try calculating the value of Resistance (with known Voltage and current) or Voltage (with known Current and resistance) using the above ohms law calculator. This calculator will also provide you the power rating of the circuit using the above formulae.